Zmiana orbity

Ocena użytkowników: 0 / 5

Gwiazdka nieaktywnaGwiazdka nieaktywnaGwiazdka nieaktywnaGwiazdka nieaktywnaGwiazdka nieaktywna
 
Szczegóły
Kategoria: Baza wiedzy

W poprzednim artykule wyjaśniliśmy czym jest orbita oraz to, jak zmienić orbitę poprzez zmianę prędkości. Jeśli jednak chcesz dostać się z orbity A na orbitę B, musisz wiedzieć jak bardzo musisz zmienić prędkość. Na szczęście podstawy nie są aż takie trudne.

Podstawowe pojęcia

Na początku warto zapoznać się z podstawowymi pojęciami, takimi jak:

  1. a - półoś wielka (ang. semi-major axis) - to połowa dystansu pomiędzy apogeum i perygeum

  2. perycentrum - najniższy punkt danej orbity, określany od środka obiektu wokół którego orbitujemy, nie jego powierzchni. Gdy ciało orbituje Ziemię, nazywamy go perygeum.

  3. apocentrum - najwyższy punkt orbity, zawsze znajduje się on dokładnie po przeciwnej stronie perycentrum. Gdy ciało orbituje Ziemię nazywamy go apogeum.

  4. r - czyli promień orbity. To dystans pomiędzy statkiem kosmicznym a środkiem ciała niebieskiego, wokół którego on orbituje.

  5. G - czyli stała grawitacji. Wynosi ona  6,674⋅10−11m3kg⋅s26,674⋅10-11m3kg⋅s2. Wyprowadza się to ze skomplikowanego równania, nie jest to istotne.

  6. e - ekscentryczność, to wartość pomiędzy 0 a 1 która określa to, jak wielka jest różnica pomiędzy apogeum i perygeum. Im większą wartość przyjmuje ekscentryczność (e), tym bardziej orbita staje się eliptyczna. Jeśli e przyjmuje wartość większą od 1, oznacza to, że statek porusza się po trajektorii ucieczkowej z danego układu.

Jeśli znasz apogeum i perygeum orbity, możesz łatwo i szybko policzyć a (półoś wielką) poprzez dodanie ich do siebie, a następnie podzielenie przez dwa. Istotne jest aby określić apogeum i perygeum od środka ciała niebieskiego oraz to, aby używać metrów a nie kilometrów czy mil. Wszystkie te wartości są ze sobą ściśle powiązane i opisane poprzez to równanie:

rp=(1−e)arp=(1-e)a

ra=(1+e)ara=(1+e)a

Gdzie rprp to promień od środka ciała niebieskiego do perygeum, a rara to promień od środka ciała niebieskiego do apogeum.

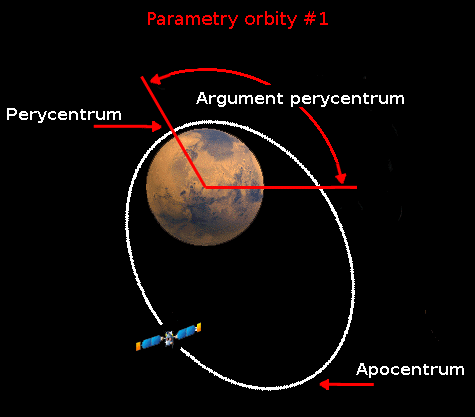
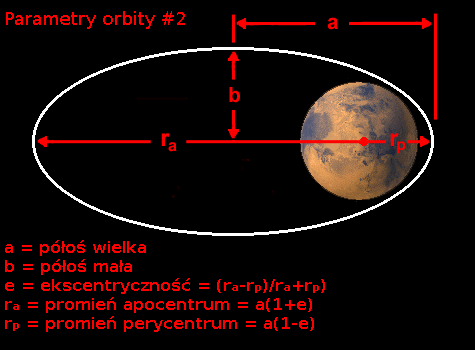
Obliczanie ∆V

Powiedzmy, że chcesz się dostać z niskiej orbity okołoziemskiej (LEO) na transferową orbitę geostacjonarną (GTO), tak jak Falcon 9 podczas większości komercyjnych misji. Aby obliczyć wymaganą ∆V, możesz zastosować następujące równanie:

v2=GM(2r−1a)v2=GM(2r-1a)

Gdzie vv to prędkość podana w msms oraz MM to masa Ziemi podana w kilogramach.

W naszym przypadku pierwotna orbita to 200x200 kilometrów nad poziomem morza, a docelowa orbita to 35876x200 kilometrów nad poziomem morza. Musimy dodać 6371 km do tych wartości, ponieważ, jak wspominałem wcześniej, do obliczeń używamy wartości określanych od środka ciała niebieskiego, w tym przypadku musimy uwzględnić promień Ziemi. Musimy również pomnożyć wszystko przez 1000, aby otrzymać wartości wyrażone w metrach. (W każdych obliczeniach możemy skorzystać z dostępnych gotowców, jak poprzednio uczyniłem w przypadku wartości G). Aby obliczyć prędkość początkową na orbicie 200 km n.p.m., musimy skorzystać z następujących równań:

v2=5,97219⋅1024⋅6,674⋅10−11⋅(26,571⋅106−16,571⋅106)v2=5,97219⋅1024⋅6,674⋅10-11⋅(26,571⋅106-16,571⋅106)

v2=60658036.92v2=60658036.92

v=√60658036.92≈7788,3msv=√60658036.92≈7788,3ms

Jeśli zrobimy to samo dla drugiej orbity, zmieniając a (półoś wielką) z 6571 km na 35786+6371+200+63712=2436435786+6371+200+63712=24364 km, albo 2,4364⋅107m2,4364⋅107m, otrzymamy prędkość v=10244,8msv=10244,8ms.

Jeśli chcemy dodatkowo otrzymać wartość ∆V dla tego manewru, musimy jedynie odjąć od prędkości końcowej prędkość początkową, otrzymamy wtedy ΔV=2456,5ms∆V=2456,5ms, co prawie dokładnie odzwierciedla realne zapotrzebowanie tego manewru na ∆V. Dla pewności podczas wykonywania tego manewru zawsze dodaje się niewielki dodatni margines błędu.